Grafos

Los grafos son estructuras geniales útiles en la representación de prácticamente cualquier cosa. Los grafos son tan útiles que se han utilizado en áreas avanzadas de matemáticas como Teoría de grafos y de informática.

• Definiciones
• Necesidad de un grafo
• Representación de un grafo
• Árboles
• Los grafos como herramientas

Definiciones

Es importante conocer algunas de las definiciones que utilizaremos.

Grafo

Conjunto de objetos llamados nodos que se relacionan entre sí a través de aristas.

Nodos o vértices

Elemento individual representado en el grafo.

Aristas o arcos

Relación entre dos nodos de un grafo

Grafo dirigido

Un grafo es dirigido cuando sus aristas tienen un sentido definido, es decir, en donde podemos llegar desde el nodo A al nodo B pero no del nodo B al nodo A.

Grafo no dirigido

Un grafo es no dirigido cuando todos sus aristas son bidireccionales, por lo que se puede ir del nodo A al B y viceversa.

Adyacencia

Dos aristas son adyacentes si tienen un nodo en común.

Dos nodos son adyacentes si una arista los une.

Incidencia

Una arista es incidente a un vértice si ésta lo conecta con otro.

Ponderación o peso

Se dice que una arista tiene una ponderación o peso determinado cuando se asocia un valor a la misma.

Etiquetado

Un nodo o arista está etiquetado cuando se le da un nombre de identificación independiente de su valor.

Orden

Un grafo es de orden \(N\) cuando tiene \(N\) nodos. También puede aplicar para las aristas.

Necesidad de un grafo

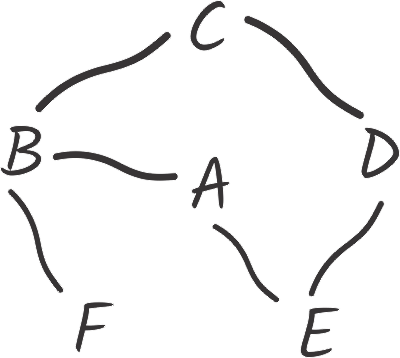
A primera instancia podría parecer que utilizar un grafo es algo innecesario, sin embargo, en muchos problemas vamos a encontrar que es la mejor opción. Un ejemplo clásico por representativo de uso de grafos es relacionar ciudades por carreteras. Como sabemos, las carreteras conectan ciudades, y no siempre hay una carretera que vaya de una ciudad a otra. Podemos identificar que hay que utilizar un grafo ya que cada elemento puede o no tener una relación de determinado tipo con otro elemento. Si representamos el mapa de ciudades conectadas por carreteras, podemos tener algo de la forma:

En donde \(A, B, C, D, E, F\) son las ciudades, y las líneas (aristas) indican que existe una carretera entre las dos ciudades que une. En este caso, podemos ir de la ciudad \(A\) a la ciudad \(B\) usando sólo una carretera.

El punto clave al momento de utilizar grafos para resolver un problema, independientemente de la metodología propia en la resolución del problema, es la forma de representación de la información en la computadora. Como imaginarás, no podemos hacer el dibujo del grafo en el compilador, y afortunadamente no es necesario.

Un grafo nos sirve para identificar que existe una determinada relación entre elementos, la forma en la que los representemos debe ser independiente de las relaciones que existen.

Representación de un grafo

Existen varias formas de representar un grafo al momento de programar, aquí explicaremos dos métodos, uno utilizando una matriz de adyacencia y otro utilizando una lista de adyacencia.

Matriz de adyacencia

Es una método muy sencillo de representar las adyacencias de nodos existentes en el grafo. Lo que hacemos es decir si entre el nodo \(A\) y el nodo \(B\) hay una arista. Para esto tenemos una matriz de \(N * N\) locaciones, donde \(N\) es la cantidad de nodos que existen en el grafo. Cada locación de la matriz corresponde al número de identificación o etiqueta de cada nodo. Por ejemplo, en nuestra imagen ejemplo de las ciudades será necesaria una ligera conversión de etiquetas, en donde el nodo \(A\) será ahora el nodo \(1\), el nodo \(B\) será el nodo \(2\) y así sucesivamente con los \(N = 6\) nodos.

Entonces para este ejemplo tendremos una matriz adyacencias[N+1][N+1] (el N+1 es porque también utilizaremos la locación N dado que hay un nodo N), en cada locación marcaremos si existe la adyacencia. Para marcar, basta con poner en esa locación un valor control que nos indique la arista existente. Para este ejemplo usaremos un 0 si no existe la adyacencia y un 1 si sí existe.

Grafo no dirigido

Para un grafo no dirigido, obtendremos una matriz que tiene como eje de simetría la diagonal central. Para nuestro grafo ejemplo tenemos:

Esto es debido a que podemos ir del nodo 1 al nodo 2 y del nodo 2 al nodo 1, y que además, como es lógico, podemos ir de la ciudad X a la ciudad X dado que es la misma. Es por eso que se forma una especie de espejo en torno a las locaciones iguales en ambas dimensiones.

Es importante tener en cuenta que en muchos algoritmos que utilizan grafos es recomendable decir que el nodo X no es adyacente al nodo X, esto es debido a que podemos generar ciclos infinitos al explorar nuestro grafo. Lo anterior aplica para todo tipo de grafos y con todo tipo de representaciones, aunque claro, si nuestra solución nos permite o incluso necesita recordar que un nodo es adyacente consigo mismo, entonces es válido hacer lo que hemos hecho en el ejemplo.

Grafo dirigido

Si por ejemplo, nuestro grafo estuviera dirigido, sólo podríamos ir del nodo A al nodo B pero no del nodo B al nodo A. Para esto marcamos sólo de un lado. Aquí podemos tomar nuestro eje x como un “desde” y nuestro eje y como un “hasta”. Un ejemplo de matriz de adyacencia en un grafo dirigido es la siguiente.

Aquí podemos ver que podemos ir del nodo 1 al nodo 4, sin embargo no es posible ir del nodo 4 al nodo 1. Nota que no hemos representado el dibujo correspondiente a la matriz de adyacencia anterior pero podemos imaginarla fácilmente dado que la matriz de adyacencia nos da la información necesaria.

Aristas con pesos

Podemos representar el peso de las aristas (en caso de que exista) utilizando el razonamiento anterior, solamente cambiamos los valores que ubicamos. En lugar de poner un \(1\) si existe la adyacencia, podemos ubicar el peso de esa arista, por ejemplo un \(5\). Los pesos de las aristas las podemos ver de forma práctica como si en esa carretera existiera una caseta de cobro. Por lo tanto para ir de una ciudad a otra tendríamos que pagar diferentes cantidades según el costo de esa caseta en esa carretera.

Si existieran pesos iguales a \(0\), es decir, que existieran casetas con precios o gratuitas, podemos ubicar como valor de no existe arista en \(-1\). La cosa es no confundir los pesos con los valores de control de la matriz.

Podemos ver que para ir de la ciudad X a la ciudad X no hay que pagar nada. Si queremos ir de la ciudad 3 a la 6 hay que pagar \(9\) y que no podemos ir de la ciudad 5 a la 6.

Lista de adyacencia

Cuando usamos una lista de adyacencia, lo que hacemos es crear un arreglo de longitud \(N\) para \(N\) nodos y en cada posición i meter los nodos adyacentes al nodo i. Es como una manera de acortar la matriz de adyacencia, al no agregar los nodos a los que no podemos ir. Por esto mismo podemos darnos cuenta, de que las listas de adyacencia funcionan igual en grafos dirigidos que en grafos no dirigidos. Para nuestro mapa de ciudades y carreteras podemos generar la siguiente lista de adyacencia:

Así podemos representar que del nodo 3 podemos ir al nodo 2 y 4, que del nodo 6 sólo podemos ir al nodo 2, etc. Puedes generar una lista de adyacencia como la anterior utilizando punteros o algunas plantillas como vector o list. Todos son válidos y su utilidad varía según el problema específico que estemos resolviendo. También puedes ponerle pesos si agregas el uso de estructuras o clases, por ejemplo.

Árboles

Los árboles son un tipo particular de grafo dirigido, en el que existe un nodo raíz del que descienden todos los demás nodos y existe un camino único para ir de un nodo a otro. Para poder entender mejor el tema de los árboles, resulta conveniente establecer algunas definiciones:

Raíz

El nodo superior del árbol.

Nodo que no tiene nodo padre.

Hijo

Un nodo es hijo respecto a otro cuando es inmediatamente descendiente del otro nodo.

Padre

Nodo que tiene hijos.

Caso inverso del hijo.

Hermanos

Nodos que comparten el mismo nodo padre.

Descendiente

Nodo accesible por descenso repetido de padres a hijos.

Ascendiente

Nodo accesible por acenso repetido de hijos a padres.

Hoja

Nodo que no tiene hijos.

Nodo externo.

Nivel

El nivel de un nodo se define como 1 + el número de conexiones entre el nodo y la raíz.

Podemos imaginarnos un árbol fácilmente como un árbol genealógico, donde el nodo raíz es el abuelo más antiguo. Tú, como hijo de tus padres serías el nodo hijo de ellos que son nodos padres respecto a ti. Si tienes hijos, tus hijos serían tus nodos hijos respecto a ti que serías nodo padre respecto a ellos. Además, si tienes hermanos o hermanas, serías un nodo hermano respecto a ellos o ellas.

El parentesco de un nodo siempre se tiene que definir con respecto a otro.

Podemos también definir un árbol utilizando listas o matrices de adyacencia, o podemos utilizar estructuras, que de hecho es muy clásico. Para un árbol binario, por ejemplo, en el que cada nodo tiene máximo dos nodos hijos, podemos definir una estructura como sigue:

Según la naturaleza de nuestro problema será también la naturaleza específica de nuestro árbol, en el que sabremos si está permitido ir de un nodo hijo a uno padre o sólo de un nodo padre a un nodo hijo. También podemos ahorrarnos el definir la variable miembro id si lo relacionamos con la locación que ocupa en el arreglo nodos. Además, en algunos algoritmos resulta especialmente útil distinguir entre el HijoIzq y el HijoDer, pues según sea el lado del que está el hijo, la relación con respecto al padre, por ejemplo, que sepamos que el HijoIzq sea menor que el HijoDer.

También podemos representar un árbol con un arreglo, en donde el identificador de cada vértice es su índice y el valor de cada locación representa al padre de cada nodo. Se da por hecho que la raíz del árbol se identifica rápidamente pues la raíz de un árbol es ese elemento del arreglo donde arbol[x] == x; para todos los demás nodos del árbol estaríamos considerando algo como arbol[x] != x;. Con este esquema podemos recorrer fácilmente cada camino de un árbol, partiendo desde las hojas. También es una forma útil de representar un árbol que no es necesariamente binario.

En el ejemplo anterior podemos ver que el nodo raíz es el 6, pues su padre es él mismo. Los hijos directos de este nodo raíz son el nodo 2 y el 7. El nodo 2 tiene un único hijo que es el nodo 3, que a su vez tiene dos hijos, el nodo 1 y el 4. Así podemos ir generando todos los caminos de nuestro árbol. También podemos guardar en el mismo arreglo diferentes árboles (que no compartan la misma raíz).

Personalmente encuentro muy útil esta clase de representación, sobretodo cuando queremos buscar pertenencias o marcar uniones. Además, se gasta menos memoria y en algunos casos su uso es más intuitivo, pero desde luego que no siempre es la mejor opción y como ya se decía, la forma de representar determinado objeto, relación o componente conexa varía según el problema que se está resolviendo.

Los grafos como herramientas

De las grandes cualidades de estas estructuras, es que su implementación estimula la capacidad del programador para identificar y aprovechar las relaciones que existen entre las distintas variables que tenemos. Identificar correctamente estas relaciones, ha permitido representar eventos muy complejos como la sinapsis en las neuronas. A medida que se practica la utilización de los grafos para resolver problemas, se podrán ir resolviendo de forma casi natural situaciones sumamente complejas.

Más adelante retomaremos estas estructuras para conocer distintas formas de recorrer cada nodo y aprovecharemos la naturaleza de las aristas para poder optimizar búsquedas y ordenamientos, entre muchas cosas más.

Cita esta página

Include Poetry - Code. (2020, 4 de enero). Grafos. Obtenido de https://www.include-poetry.com/Code/C++/Estructuras/Grafos/