Dynamic Programming

Cuando buscamos una solución que requiere del cálculo de muchas posibles soluciones, solemos intentar utilizando una estructura recursiva, una búsqueda completa o exhaustiva. Sin embargo, en ocasiones, nuestro árbol recursivo genera la respuesta a un mismo problema muchas veces, lo que incrementa el tiempo de ejecución, para evitar este problema podemos recurrir a la técnica de Programación Dinámica o DP.

• Condiciones para la DP
• Confirmando el uso de DP
• Tamaño de la tabla de DP
• Partiendo de una solución recursiva
• Generando una solución iterativa
• Memoization

Condiciones para la DP

Las condiciones para considerar una DP son las siguientes:

• El problema tiene subestructuras óptimas: es decir, se puede solucionar de forma óptima el problema a partir de fragmentarlo en subproblemas y tomar la solución óptima de cada uno.
• La solución del problema tiene casos que se sobreponen: reconstruimos una misma solución varias veces.

Generalmente nos damos cuenta que un problema requiere el uso de DP cuando se podría resolver con una búsqueda completa pero que no cumpliría en tiempo y nos damos cuenta que no cumpliría en tiempo cuando evaluamos los límites del problema y dada la complejidad de la búsqueda completa o exhaustiva reconocemos que no podremos cumplir.

Confirmando el uso de DP

Se puede confirmar el uso de una DP cuando evaluamos el árbol recursivo que generaría la búsqueda exhaustiva. Por ejemplo, retomemos el problema de la compra de panes de diferentes categorías.

Vamos a una panadería en donde venden \(t\) diferentes tipos de panes, de cada tipo se tiene \(x_i\) cantidad de panes, se tiene además el peso específico de cada uno de esos panes. La intención es comprar un pan de cada categoría gastando lo más posible de un presupuesto \(d\). Trabajaremos con el siguiente ejemplo de entrada:

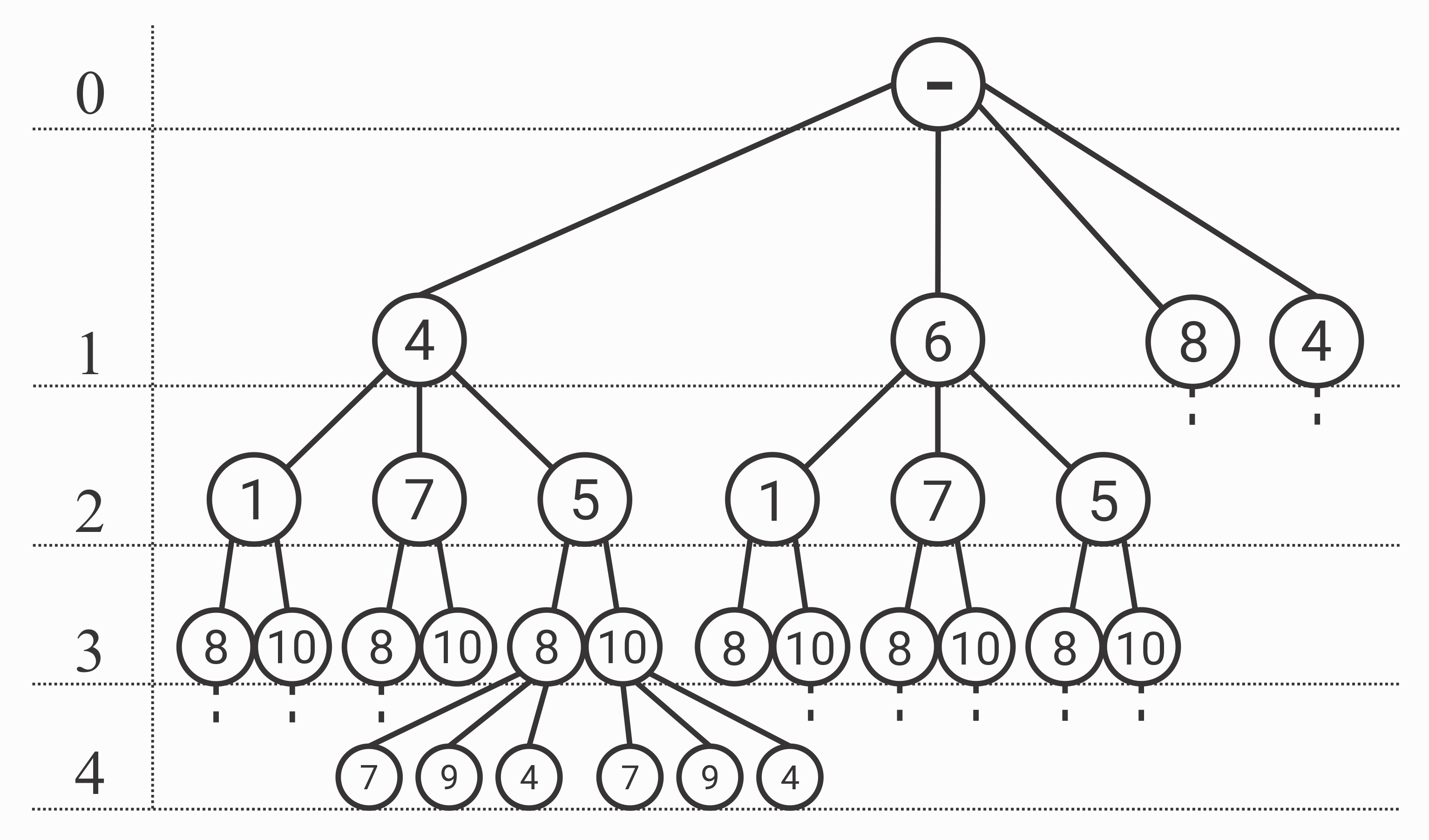
Entonces, hay \(4\) tipos de panes, tenemos un presupuesto de \(30\), la primer categoría tiene \(4\) elementos de precios \(6, 2, 8, 4\), la segunda categoría tiene \(3\) elementos de precios \(1, 7, 5\) y así sucesivamente. Si realizamos una búsqueda exhaustiva sobre las distintas opciones de compras de los panes obtendríamos un árbol como el siguiente:

Del lado izquierdo se especifican las diferentes profundidades de éste árbol. Dentro del árbol hay líneas que son punteadas y cortas, con ellas quiero dar a entender que el árbol continúa, que las opciones no se acaban ahí.

Las profundidades también estarían respondiendo al problema si tuviéramos únicamente las primeras \(k\) categorías, por ejemplo, si tuviéramos sólo cero categorías para comprar, lo mejor sería comprar… ¿nada? En realidad no tendríamos nada para comprar. Si tuviéramos \(1\) categoría entonces lo ideal sería comprar el pan de \(8\) (recuerda que el objetivo es \(30\)). Si evaluáramos con las primeras \(2\) categorías entonces la cosa se empieza a complicar, pero hasta este punto la solución greedy podría seguir funcionando, compramos ahora el pan de \(7\) y entonces llegamos a la solución óptima. Sin embargo, a medida que añadimos más categorías podemos ver que la solución greedy no es efectiva.

En la búsqueda a profundidad podríamos ver todos los posibles caminos de ese árbol recursivo, todas las posibles opciones de compra, esto se tomaría mucho tiempo, en este ejemplo estaríamos generando los \(4 * 3 * 2 * 3\) posibles caminos del árbol recursivo. Esto sin duda genera la solución, pero tardaría mucho cuando los límites incrementan.

Ahora sí, podemos notar en el árbol recursivo que muchos caminos se están repitiendo, podemos ver que de la profundidad \(2\) hacia abajo (hacia la profundidad \(4\)) todo se repite, para cada elemento de la categoría \(1\) (para cada vértice de la primera profundidad) vamos a generar todos los mismos caminos hacia abajo, todo esto se computa cada vez en la búsqueda exhaustiva, cuando en realidad podríamos ahorrárnoslo en tiempo de ejecución.

Si generamos una parte del árbol y la guardamos, luego que sigamos generando las opciones del árbol recursivo y que necesitemos de una parte igual a esa que generamos antes y la recordamos de ese lugar donde lo guardamos, entonces ya no tendremos que generarlo de nuevo, nos ahorramos ese tiempo de ejecución y por lo tanto nuestra solución es mucho más eficiente.

Tamaño de la tabla de DP

Como queremos asociar cada estado con una solución, es importante que podamos calcular bien el tamaño de la estructura que guardará nuestras soluciones. Lo importante aquí es identificar cuántos parámetros o aspectos definen un estado como el que usamos en la búsqueda, de ahí podemos generar una estructura en donde podamos asociar rápidamente el valor de cada parámetro con la respuesta del estado que forman esos parámetros en cuestión.

Si estamos generando una solución donde cada estado se determina por \(2\) parámetros \(a\) y \(b\) entonces podemos utilizar una matriz, donde en una dimensión de esa matriz podamos asociar el parámetro \(a\) y en la otra dimensión asociemos el parámetro \(b\). Es importante ahora cuidar que esa matriz (y en sí cualquier estructura que usemos para los estados) se pueda generar con los límites de memoria que nos otorga el problema.

Si nuestra solución considera estados de \(3\) parámetros entonces necesitaremos un arreglo de \(3\) dimensiones y por lo tanto la cantidad de parámetros diferentes debe ser lo suficientemente pequeña para que ese arreglo sea posible. Como puedes ver, lo que limita a una DP generalmente es la memoria con la que contamos.

Partiendo de una solución recursiva

Podemos empezar a generar nuestra solución DP si partimos de nuestra solución recursiva. Podemos ir generando los caminos de forma recursiva siempre y cuando identifiquemos y recordemos las soluciones ya generadas anteriormente. Entonces, para este ejemplo primero generaremos la solución de búsqueda exhaustiva, además sirve como repaso de esta metodología.

Construyendo la búsqueda exhaustiva

Entonces, lo primero es ver cómo vamos a guardar nuestra entrada, en este caso vamos a guardarlo todo en una matriz. En la matriz categorías[x][y] vamos a meter en la primera dimensión (la de [x]) la cantidad de categorías. En la dimensión de [y] vamos a meter los elementos de la categoría \(x_i\). Vamos a rellenar esta matriz como sigue:

Ya que tenemos los datos la matriz podemos pasar a formular la búsqueda total o exhaustiva. Lo primero que vamos a hacer es ir de categoría en categoría tomando un elemento. Entonces tenemos que considerar en cada estado la categoría de la que estamos tomando. Lo que sigue es considerar la cantidad de dinero que hasta ese momento hemos gastado. Estas son las partes que conforman cada estado de la búsqueda.

Ahora podemos ver que vamos a intentar tomar cada uno de los elementos de cada categoría. Entonces cada que entremos a una categoría vamos a dejar pendiente el procesar cada uno de los elementos de esa categoría. Lo que sigue es darnos cuenta que no podemos gastar una cantidad mayor al presupuesto que tenemos (esto es una poda, claro) entonces cada que exploremos una opción tenemos que saber que el dinero gastado hasta ese momento es factible.

Sabremos que hemos terminado un camino del árbol si ya hemos tomado de cada una de las \(t\) categorías (si ya hemos visitado todas las profundidades del árbol). En ese momento podemos evaluar si la cantidad de dinero gastado siguiendo esas opciones de compra (ese camino del árbol) es la mejor respuesta que podemos formar. Siguiendo todo lo anterior entonces podemos formar el siguiente código:

Entonces ya tenemos nuestra solución recursiva que explora todos los caminos posibles del árbol. Esto, como ya se decía, es tardado y no da en tiempo cuando aumentamos nuestros límites. Lo que ahora tenemos que hacer es encontrar el momento en el que tenemos que guardar una posible solución y el momento en el que podemos recordar un camino ya formado.

Formando la DP

Si somos atentos, podemos notar que para cada estado hay una solución única y óptima (por el mismo principio que dice que hay un sólo camino que va de la raíz a cada vértice de un árbol). Entonces podemos guardar una respuesta por cada estado. Para esto podemos tener una tabla (la famosa tabla de DP) en la cual podemos guardar para cada estado una solución óptima. Nota que es una matriz (\(2\) dimensiones) porque cada estado se define por dos parámetros, el dinero gastado hasta ese momento y la cantidad de categorías de las que podemos escoger.

El momento en el que guardamos algo en nuestra tabla de DP es justamente el momento en que nuestra recursión genera una opción y en efecto es la mejor opción. Ahí podemos guardar en nuestra tabla en la posición que muestra el estado con el que llegamos. Así podríamos leer nuestra tabla DP[dineroGastado][categoriaAlcanzada] como “puedo gastar hasta \(dineroGastado\) si compro hasta la categoría \(categoriaAlcanzada\)”. Entonces estaríamos generando todas las posibles mejores opciones para cada estado en nuestra tabla y ya tendríamos la respuesta.

Entonces si identificamos en nuestro código recursivo podemos ver que la solución se genera en la línea 5. Ese momento en que actualizamos nuestra mejor solución según la nueva cantidad máxima. Esa solución máxima está dada por un estado particular. Ese estado particular se ubica en la tabla DP y entonces ya la tenemos guardada para cuando volvamos a pasar por ese estado.

Ahora sí podemos pensar en qué momento debemos recordar una solución ya calculada. Si el estado que estamos evaluando en un momento dado ya está registrado en la tabla DP entonces en lugar de seguirlo generando tenemos que tomarlo de la tabla y listo.

Nota que no sólo estamos generando las opciones del árbol recursivo sino que además nos estamos quedando en la tabla de DP únicamente con los mejores resultados de cada profundidad. Puedes explorar cómo se genera la tabla y cómo se va modificando conforme vamos considerando cada opción si imprimes DP[][] luego de la línea 11. Podrás notar que se generan diferentes resultados y se van actualizando conforme continúa la búsqueda de la solución.

Generando una solución iterativa

Para solucionar el problema anterior de forma iterativa, podemos explorar todas las opciones de una forma distinta. En lugar de ir viendo qué solución sería la mejor en cada profundidad podemos ir generando todas las soluciones posibles para cada cantidad de objetos que podamos tomar. Revisamos si es posible comprar \(g\) objetos con una cantidad \(h\) de dinero.

Entonces lo primero que haríamos sería ver el resultado de utilizar cada una de las opciones de la primer categoría, luego, para cada gasto resultante vemos el resultado de tomar cada uno de los elementos de la segunda categoría y así con todas. Utilizaremos la misma estructura categorias[][] que usamos en el ejemplo recursivo.

Al final habremos generado una tabla que muestra para cada profundidad la cantidad de dinero posible que se puede generar si compramos todas las posibles combinaciones de objetos hasta esa categoría. Entonces, la mayor cantidad posible para gastar se encontrará al final de todos los valores de la última profundidad (es decir, de haber tomado hasta de la última categoría).

Para encontrar este valor máximo lo que podemos hacer es recorrer fila de la última categoría (t-1 porque las categorías se indexaron en \(0\)) desde atrás hacia adelante, es decir, desde la cantidad equivalente al presupuesto inicial (d) hacia el \(0\), porque en el mejor de los casos gastamos exactamente \(d\) y conforme nos acercamos a \(0\) (o nos alejamos de \(d\)) entonces menos óptima es la respuesta. Si nos pasamos de \(0\) entonces nunca hubo una combinación de elementos seleccionados que nos permitieran comprar un elemento de la última categoría, es decir, no se puede resolver el problema. Esto se puede implementar como sigue:

Como puedes notar se deja la condición res>=0 dentro de while, la parte del = es para que pueda bajar de \(0\) si no hay respuesta y entonces sea posible identificar un estado de solución imposible gracias a un típico valor -1.

En este ejemplo recursivo no es tan obvia ese proceso de guardar un camino ya generado y recordarlo después, pero seguimos generando las posibles opciones y seleccionando la mejor, además de que seguimos cumpliendo en tiempo.

Memoization

Memoization es un término en inglés que no resulta sencillo de traducir al español. Se refiere a esta técnica de optimización en la que realizamos ese proceso de guardar el resultado de un proceso de cómputo para recordarlo después si es que nos lo volvemos a encontrar. En la literatura este término es muy común, es por ello que considero importante que lo conozcas y sepas a qué se está haciendo referencia.

Cita esta página

Include Poetry - Code. (2020, 4 de enero). Dynamic Programming. Obtenido de https://www.include-poetry.com/Code/C++/Metodos/DP/