Unión y pertenencia

Cuando se platicaba de árboles se decía que un árbol tiene un nodo al cuál llamamos raíz, que es el único que no tiene padres y origina al resto de la componente conexa. Para saber si dos nodos son partes de una misma componente conexa (o tienen el mismo origen) se pueden realizar operaciones de pertenencia y para unir dos componentes conexas distintas podemos utilizar uniones.

• Definiendo cada término
• Estructura de ejemplo
• Pertenencia
• Unión
• Optimizando los procedimientos
• Diferentes comienzos
• Conclusión

Definiendo cada término

Podemos definir la unión y la pertenencia como sigue:

Unión

Método en el que se unen dos componentes conexas distintas

Procedimiento por el cual se unen dos nodos a través de una arista

Pertenencia

Método con el que se puede saber si dos nodos distintos forman parte de la misma componente conexa.

Nota que nos referimos a una componente conexa en ambos casos y no sólo a un grafo o a un árbol. Estas operaciones definidas arriba deben ser diseñadas para ser eficientes y que nos permitan actualizar un árbol de expansión rápidamente. Estas operaciones no pueden recaer en búsquedas como las que ya conocemos, pues nos tomaría más tiempo del que disponemos.

Recuerda que todo grafo dirigido tienen un árbol de expansión, es decir, podemos ir de un nodo a otro siguiendo un camino particular que responde a determinantes específicas. Para poder utilizar las funciones de unión y pertenencia como las vamos a definir es importante tener en claro que hay que utilizar una estructura que represente fácilmente un árbol.

Estructura de ejemplo

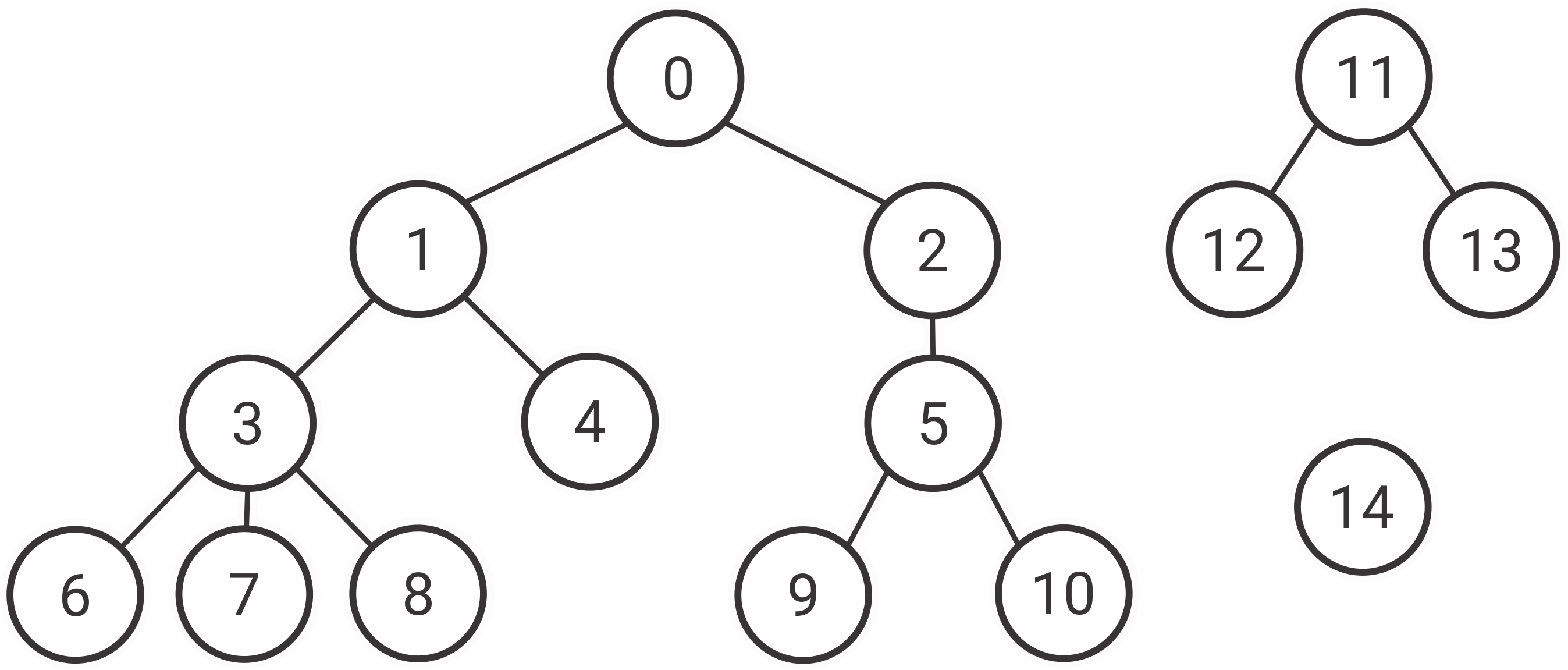
La estructura que vamos a utilizar en estos ejemplos es un árbol (precisamente el árbol de expansión en caso de que hablemos de grafos dirigidos). Este árbol no tiene que ser especialmente binario o completamente balanceado. Se representará en la computadora utilizando un arreglo arboles[] en donde la locación \(i\) se guarda el idenficador del padre de \(i\), es decir, con arboles[3] = 5 se da a entender que el vértice \(3\) es hijo del vértice \(5\). Representaremos el siguiente grupo de árboles en un arreglo:

Como puedes ver, el índice del arreglo nos dice el vértice en cuestión, el valor del arreglo en ese índice nos dice quién es el padre de ese vértice. El nodo raíz se caracteriza por ser el nodo x donde arboles[x] == x, es una forma de marcar que la raíz no tiene padre. También se puede utilizar un valor control como -1, pero personalmente prefiero el método arboles[x] = x.

Pertenencia

Podemos plantearnos la pregunta ¿el nodo \(a\) pertenece al mismo árbol que el nodo \(b\)?, es decir, ¿hay algún camino que una a \(a\) y \(b\)? Podemos saber si un vértice pertenece a la misma componente conexa que otro si ambos comparten la misma raíz.

Recordemos que, en un árbol cuando existe un camino que une al vértice \(a\) con \(b\) éste camino es único.

Entonces este problema se enfoca a encontrar la raíz del vértice \(a\) y del vértice \(b\) y revisar si son iguales. Para encontrar la raíz del árbol que contiene a cualquier vértice sólo hay que ir subiendo de hijo a padre hasta que el vértice que estemos revisando tenga como padre a sí mismo. Realizar esto es una tarea muy sencilla dada la forma en la que guardamos nuestro árbol. De forma recursiva podemos hacer lo que sigue:

La función recibe como parámetro el vértice del cual estamos buscando su raíz. Si un vértice guarda en su posición dentro de arboles[] su mismo valor entonces quiere decir que es una raíz, por esta razón si el vértice en cuestión no es su propio padre (no es raíz) entonces buscamos la raíz de su padre (lo que me refiero con ir subiendo). Al final la función regresa el identificador del nodo raíz del árbol (o componente conexa) al que pertenece x.

La función de pertenencia es muy sencilla ahora. Lo que esta función responde es ¿\(a\) pertenece a la misma componente conexa que \(b\)? Que es lo mismo que preguntarse ¿hay algún camino que una a \(a\) con \(b\)? La función entonces se puede escribir como:

Unión

Si tenemos dos componentes conexas distintas (con raíces diferentes) entonces podemos unirlas utilizando una función de unión. Esta función lo que hará será unir las raíces de los dos árboles en cuestión. De forma más práctica lo que hacemos es unir la componente conexa a la que pertenece \(a\) con la que pertenece \(b\). Podemos realizar una unión como sigue:

Como puedes ver la raíz del árbol al que pertenece \(a\) ahora tiene como raíz la raíz del árbol al que pertenece \(b\). Esto quiere decir que ahora la raíz de \(b\) (raizB) es la raíz del nuevo árbol. ¿Es el orden de esta asignación de nueva gran raíz importante? La respuesta es sí. No sólo importa el problema que estemos resolviendo, sino también importa la complejidad.

Si unimos un árbol de profundidad \(x\) con un árbol de profundidad \(y\) y además \(x \geq y\) entonces tendremos un nuevo árbol de profundidad \(x+1\) (porque agregamos un nodo extra en la parte superior, ese nodo extra será la nueva gran raíz). En caso contrario, si \(x < y\) vamos a tener un árbol de profundidad \(y\). Debido a esto, lo mejor es que el árbol de menor profundidad apunte (se una) al árbol de mayor profundidad, así tendremos un árbol de una altura más óptima.

Optimizando los procedimientos

Podemos realizar un mejor trabajo si cuando unimos dos componentes conexas unimos cada vértice directamente a la nueva raíz. Claro, eso se hace si nos podemos permitir realizar este movimiento en la solución del problema que estemos resolviendo, puede que no siempre lo mejor sea unir todos los vértices de un árbol directamente a la raíz del nuevo árbol, pero cuando esto es permitido y es útil entonces nos ahorramos mucho tiempo en el futuro.

Esta es una forma eficiente de hacerlo, pues desde que vamos revisando cada vértice vamos dejando pendiente en la recursión el actualizar la raíz.

Diferentes comienzos

Puede que no siempre empecemos con árboles de más de un vértice ya formado, de hecho esto es algo común. Generalmente vamos analizando un grafo dirigido y conforme generamos su árbol de expansión vamos realizando las uniones respectivas. En este caso nuestro árbol debe ser inicializado antes de realizar cualquier operación de unión o de pertenencia. Para inicializarlo todos los vértices serán vértices individuales, es decir arboles[i] = i. Esto se puede realizar fácilmente con un ciclo for que itere con todos los vértices.

Conclusión

Las operaciones de unión y pertenencia son bastante útiles cuando estamos actualizando las relaciones entre componentes conexas. Por ejemplo, en una red social donde unos usuarios son seguidores de otros podemos ver relaciones de pertenencia. Cada que uno sigue a otro se forma una nueva unión.

También se puede ver en algunas redes de venta por catálogo, donde diferentes redes de vendedores trabajan para diferentes personas, cuando alguien se hace empleado de otra persona entonces él y toda su red se hacen trabajadores de esa nueva persona, aquí es cuando hacemos uniones sin actualizar cada nodo directamente a la raíz.

Las operaciones como las hemos definido tienen una complejidad bastante eficiente y soportan ser llamadas muchas veces en un mismo programa cumpliendo en tiempo y en memoria.

Cita esta página

Include Poetry - Code. (2020, 4 de enero). Unión y pertenencia. Obtenido de https://www.include-poetry.com/Code/C++/Estructuras/Grafos/Union-y-pertenencia/